Exploring the Application of Peer-assisted Learning in Hong Kong Mathematics Education (2025-2027)
Principal Investigator. Seed Fund for Basic Research for New Staff (HK$150,000). Funded by The University of Hong Kong.
Peer-assisted learning has been widely implemented in diverse educational contexts to support students’
learning from their peers. Extant research has demonstrated empirical evidence supporting the affordances of
this form of learning in students’ learning outcomes. However, most research has adopted quantitative research
methods, and little is known about the qualitative nature of student-student interactions and the affordances and
challenges students experience during peer-assisted learning. This project aims to address these research gaps by investigating the application of peer-assisted learning in Hong Kong mathematics education. Specifically, the research objectives include: (1) to support Hong Kong teachers’ implementation of peer-assisted learning at local schools, (2) to support students to implement peer-assisted learning to facilitate each other’s mathematical learning, (3) to characterise the qualitative nature of student-student interactions during peer-assisted learning, and (4) to investigate the affordances and challenges of peer-assisted learning in the context of mathematics learning.

Investigating and Supporting Students’ Mathematical Modelling Through the Quantitative Reasoning Perspective (2025)
Principal Investigator. Faculty Research Fund (HK$60,000). Funded by the Faculty of Education, The University of Hong Kong.
Mathematical modelling is recognized as both a means and an end to learning mathematics. Existing research has identified key processes involved in students’ model-building activities, such as mathematising, interpreting, and validating. While these studies provide valuable observational descriptions of students’ model construction
processes, there remains a gap in understanding how students mentally conceive and abstract
mathematical attributes from real-life situations. This project aims to provide a detailed cognitive account of students’ model construction processes through the lens of quantitative reasoning. The research objectives are twofold:
1. To characterize how students interpret real-world situations and identify relevant quantitative
attributes as they engage in open modelling tasks;
To characterize how students construct mathematical representations (e.g., diagrams, equations, graphs) to facilitate the development of mathematical relationships among the identified quantities.

Innovating Programming-enhanced Mathematics Curriculum Through Teacher-researcher Partnership: Design-based Research as a Pathway to Teachers’ Professional Learning (2024-2026)
Principal Investigator. Seed Fund for Basic Research for New Staff (HK$93,040). Funded by The University of Hong Kong.
The significance of teacher professional learning (TPL) has been widely acknowledged in the field of mathematics education. Confronted with the need to solve practical educational problems and encourage scientific inquiry, design-based research (DBR) has been employed in many TPL programmes to develop instructional innovation in real classrooms. In response to the digital age, mathematics educators and researchers are paying increasing attention to the integration of technology in mathematics education, and programming is one of the popular technological means for supporting meaningful mathematical learning. As DBR is an essential and scientific process of developing curriculum and classroom innovation, this study seeks to create a teacher-researcher partnership focused on the development of a programming-enhanced mathematics curriculum through integrating DBR in a TPL programme.
The overall goal of this proposed study is to characterise mathematics teachers’ experience during the implementation of DBR and its impact on their professional learning. Specifically, this study aims to answer three research questions: (1) How do mathematics teachers implement DBR to innovate mathematics teaching and learning with programming tools? (2) How does mathematics teachers’ engagement with DBR impact their professional knowledge for teaching? (3) How does mathematics teachers’ engagement with DBR support their reflective and inquiry stance towards mathematics teaching and student learning?

Leveraging the Affordances of Programming Environments to Develop Conceptual Mathematics Curriculum (2024)
Principal Investigator. Faculty Research Fund (HK$60,000). Funded by the Faculty of Education, The University of Hong Kong.
The first research objective is focused on identifying potential mathematical topics of which student learning could be enhanced by programming integration. Prior research has identified the affordances of programming in learning mathematical ideas across content domains, including algebra, geometry, calculus, and probability and statistics. In the proposed project, the PI will conduct a comprehensive review of the topical areas in secondary mathematics curriculum and identify a subset of key concepts as the focus of task design. The second research objective is to develop a set of innovative activities around the selected topics through iterative design, implementation, and revision. The design will be focused on supporting students’ construction of conceptual understandings of major mathematical ideas that have been considered to be challenging to students. Such design will not only be based on conceptual analysis from the researcher’s perspective but also take into account the PI’s prior work on student thinking in both programming-enhanced mathematical environments and pure mathematical environments. Upon completion of the design and implementation cycles of the instructional activities, the PI will develop design principles for integrating programming into mathematical task design. These principles will provide guidelines for future researchers and educators to effectively design programming-based instructional activities productive for students’ mathematical learning.

Collaborating with Generative Artificial Intelligence (AI) to Transform Learning and Teaching (2023-2026)
Co-Investigator. Fund for Innovative Technology-in-Education (HK$250,000). Funded by University Grants Committee (Hong Kong). P.I.: Chun Lai
Coming soon.

Investigating Interplays Between Computational Thinking and Mathematical Thinking (2023-2025)
Principal Investigator. Seed Fund for Basic Research for New Staff (HK$150,000). Funded by The University of Hong Kong.
Recent Hong Kong and worldwide curriculum reforms have called for integrating information technology in mathematics teaching and learning. As one active response to the call, mathematics educators and researchers are paying increasing attention to the role of computational thinking (CT) in supporting mathematical learning. Despite the fruitful evidence of the productive outcomes of CT-enhanced mathematics learning, few research offers nuanced analyses of the learning mechanisms entailed in CT-integrated mathematics learning at a cognitive level. The overall goal of this proposed study is to investigate how learners’ computational thinking and mathematical thinking mutually influence each other. Specifically, the PI aims to answer two research questions: (1) How do individuals apply their mathematical thinking to construct computational artifacts? (2) How does individuals’ computational thinking engender their mathematical learning? The study will focus on two population groups: secondary mathematics students and secondary pre-service mathematics teachers in Hong Kong. The collective findings will offer insights into how students and pre-service teachers reason with mathematical and computational ideas in integrated environments, which will provide important implications regarding how to support CT-enhanced mathematics learning in classrooms and how to prepare future teachers to enact this form of teaching.

Learning to Conduct Constructivist Teaching Experiment: A Collaboration with Graduate Students, Pre-service Teachers, and In-service Teachers (2023-2024)
Principal Investigator. Faculty’s Project-based Research Funding (HK$60,000). Funded by the Faculty of Education, The University of Hong Kong.
Constructivist teaching experiment (Steffe & Thompson, 2000; hereinafter referred to as CTE) is a powerful research methodology for researchers to investigate individuals’ thinking about certain concepts. Recent work in teacher education has provided evidence that in-service and pre-service teachers benefited from conducting CTE or clinical interviews to understand individual students’ thinking. However, few researchers focus on characterising the process by which individuals learn to adopt a researcher mindset to inquire into student thinking, including making decisions and actions that enable such inquiry. This study aims to investigate how different individuals (e.g., graduate students, in-service teachers, pre-service teachers; hereinafter all referred to as student researchers) learn to conduct constructivist teaching experiments and how such experiences might benefit their professional learning.
Supporting Hong Kong Ethnic Minority Learners’ Multimodal Mathematics Learning Through Responsive Teaching in Technology-Enhanced Environments 利用動態數學環境科技支援少數族裔學生的數學思維和教師相應的教學研究 (2021-2023)
Funded by the General Research Fund, Research Grants Council (Hong Kong)
PI: Oi-Lam Ng @ The Chinese University of Hong Kong
This study’s dual aims are: (1) to develop Hong Kong teachers’ expertise in supporting ethnic minority (EM) students’ mathematical learning in multimodal, technological learning environments, (2) to uncover EM students’ competences in mathematical activities in touchscreen-based dynamic and multi-representational environments through examining their multimodal discourse (e.g. words, gestures, and touchscreen dragging).
Mathematical Problem Solving through Digital Making: Envisioning a Computationally Enhanced Mathematics Curriculum in Hong Kong’s Primary and Secondary Schools 數學解難中的「造中學」:預視香港中小學中融合計算思維的數學課程 (2020-2023)
Co-investigator. Funded by the General Research Fund, Research Grants Council (Hong Kong)
PI: Oi-Lam Ng @ The Chinese University of Hong Kong
Computational thinking (CT) is a powerful cognitive tool for solving problems, designing systems, and understanding human behaviour by drawing on concepts fundamental to computer science. This study builds on the PI’s previously developed conception of “learning as Making” to envision a computationally enhanced mathematics curriculum—one that supports mathematical problem solving through digital Making (dM). Digital Making involves students’ active creation of both digital and tangible artefacts through block-based programming with physical input sensors and output devices. CT concepts and practices such as sequences, variable-naming, abstraction, algorithmic thinking, decomposing, and iterating are highlighted during problem-based dM activities, through which scientific inquiry, mathematical thinking, and engineering design can also be exhibited as integrated STEM learning. In this design-based study, a total of 20 lessons with problem-based dM tasks are developed with content appropriate to senior primary and junior secondary mathematics curricula. Findings will contribute to extending academic and professional knowledge about learning mathematics with computational tools, in response to CT and Making as a social movement. Ultimately, it will provide evidence-based directions of enhancing CT as a new literacy and problem solving as a global competence in school settings.
Relevant Publication:
Ye, H., Liang, B., Ng, O., & Chai, C. S. (2023). Integration of computational thinking in K-12 mathematics education: A systematic review on CT-based mathematics instruction and student learning. International Journal of STEM Education, 10, Article 3. https://doi.org/10.1186/s40594-023-00396-w
Hong Kong Pre-Service Teachers' Transition Between School and University Mathematics (2021-2022)
Collaborative work with Oi-Lam Ng
Relevant Publications:
Liang, B., Ng, O., & Chan, Y. (2022). Seeing the continuity behind “double discontinuity”: Investigating Hong Kong prospective mathematics teachers’ secondary–tertiary transition. Educational Studies in Mathematics. Advance online publication. https://doi.org/10.1007/s10649-022-10197-7
Ng, O., Liang, B., Chan, A., Ho, T. C., Lam, L. P., Law, M. H., Li, E. M., Lu, T. Y (2022). A collective reflection on the transition from secondary to university mathematics through the lens of the “double discontinuity” by Felix Klein. EduMath, 45.
Hong Kong In-Service Teachers' Video-Aided Reflections on Teaching and Learning with 3D Pens (2020-2021)
Collaborative work with Oi-Lam Ng and Allen Leung
This study examines the processes by which video-aided reflections may guide teachers to become aware of and develop expertise in the use of a novel-to-them technology in mathematics classrooms. Four mathematics teachers participated in this study aimed at exploring teachers’ initial experience of using and planning lessons with the technology of “3D Pens”, which enables learners to construct 3D models instantly via moving one’s hands. We analyse the participants’ reflections and interpretations of students’ actions during semi- structured interview sessions while they were watching video episodes of a lesson integrating 3D Pen for mathematics teaching and learning. Adopting the constructs of first- and second- order models, we provide fine-grained characterisation of the teachers’ mathematical and pedagogical learning in the moment of their reflection. The results suggest that the teacher participants not only shifted from operating on their first-order models to constructing second-order models of students’ geometrical thinking as supported by 3D Pens, but they also reasoned pedagogically based on their second-order models. Hence, watching videos of authentic technology-rich lessons facilitated a productive noticing experience for mathematics teachers in terms of realising the educational potential for the technology of the 3D Pens.
Relevant Publication:
Ng, O., Liang, B. & Leung, A. (2023). Using first- and second-order models to characterise in-service teachers’ video-aided reflection on teaching and learning with 3D Pens. In A. Clark-Wilson, O. Robutti, & N. Sinclair (Eds.), The Mathematics Teacher in the Digital Era (2nd ed.). Springer.
In-Service Teachers' Constructions of Knowledge of Students' Mathematical Meanings Through Student-Teacher Interactions (2019-2021)
Dissertation project @ University of Georgia
Teacher knowledge of students’ mathematical thinking has been a growing research area in mathematics education. However, teacher knowledge and student-teacher interaction are often treated as disparate research areas, and research on their interplay is sparse. This is partly due to a lack of theory and methodology that support research inquiry into teacher’s ongoing mathematical development through social interactions with students.
In this dissertation, I expanded the constructivist teaching experiment methodology to a methodology called teaching experiment^2 and implemented it with two high school teachers and three of their students. Adopting and integrating radical constructivism, Piagetian learning theories, and communication theories, I propose a framework of teacher decentering that specifies the cognitive mechanisms by which teachers construct knowledge of students’ mathematics and reorganize their personal mathematical knowledge. The findings contribute to an operationalization of anti-deficit, constructive, and dynamic perspectives on teacher knowledge and knowing. They also inform teacher educators of specific mental processes they can foster as they support teachers’ mathematical learning in relation to student thinking.
Dissertation Committee: Kevin C. Moore (Chair), Amy Ellis, Cameron O’Neill Byerley, Jaime Marie Diamond, Carlos Castillo-Garsow
Doctoral Dissertation:
Liang, B. (2021). Learning about and learning from students: Two teachers’ constructions of students’ mathematical meanings through student-teacher interactions (Publication No. 28410786) [Doctoral dissertation, University of Georgia]. ProQuest Dissertations & Theses Global.
CAREER: Advancing Secondary Mathematics Teachers' Quantitative Reasoning (2015-2020)
NSF Award #1350342. PI: Kevin Moore @ University of Georgia
Advancing Reasoning addresses the lack of materials for teacher education by investigating pre-service secondary mathematics teachers' quantitative reasoning in the context of secondary mathematics concepts including function and algebra. The project extends prior research in quantitative reasoning to develop differentiated instructional experiences and curriculum that support prospective teachers' quantitative reasoning and produce shifts in their knowledge. Three interrelated research questions guide the project: (i) What aspects of quantitative reasoning provide support for prospective teachers' understanding of major secondary mathematics concepts such as function and algebra? (ii) How can instruction support prospective teachers' quantitative reasoning in the context of the teaching and learning of major secondary mathematics concepts such as function and algebra? (iii) How do the understandings prospective teachers hold upon entering a pre-service program support or inhibit their quantitative reasoning?
Online Curriculum:
Moore, K. C., Liang, B., Tasova, H. I., & Stevens, I. E. (2019). Advancing reasoning covariationally (ARC Curriculum). Athens, GA. https://sites.google.com/site/advancingreasoning/arc-curriculum
Relevant Publications:
Moore, K. C., Liang, B., Stevens, I. E., Tasova, H., & Paoletti, T. (in press). Abstracted quantitative structures: Using quantitative reasoning to define concept construction. In G. K. Akar, İ. Ö. Zembat, S. Arslan, & P. W. Thompson (Eds.), Quantitative Reasoning in Mathematics and Science Education. Springer.
Liang, B. & Moore, K. C. (2021). Figurative and operative partitioning activity: Characterizing a student’s meanings for amounts of change. Mathematical Thinking and Learning, 23(4), 291-317. https://doi.org/10.1080/10986065.2020.1789930
Moore, K. C., Stevens, I. E., Paoletti, T., Hobson, N. L. F., & Liang, B. (2019). Pre-service teachers’ figurative and operative graphing actions. The Journal of Mathematical Behavior, 56, Article 100692. http://doi.org/10.1016/j.jmathb.2019.01.008
GAMMA: Generalization Across Multiple Mathematical Areas (2016-2017)
NSF Award #1419973. PI: Amy Ellis @ University of Georgia
The recommendation to make generalization a central component of mathematics instruction from elementary school through undergraduate mathematics poses serious challenges in light of the research base that identifies students' difficulties in creating and expressing correct mathematical generalizations and the challenges teachers face in supporting students' abilities to generalize. Furthermore, although student difficulties are well documented, the instructional conditions necessary for fostering generalization are not well understood, particularly at the secondary and undergraduate levels. This project addresses these challenges by developing a comprehensive framework characterizing productive mathematical generalization in Grades 8-16 and identifying instructional interventions that can support correct generalizing. The project occurs within multiple mathematical domains extending from middle school to undergraduate mathematics, including algebra, geometry, calculus, and combinatorics. The project investigators will leverage student interviews, teaching experiments, and design experiment methodologies in order to characterize the processes of generalizing and to identify the instructional conditions that support productive generalization. The results of the project will identify specific tasks and activities fostering student generalizing in a diversity of mathematical settings, which will be of practical use to teachers, school districts, teacher educators, and university instructors.
A Review of Quantitative Reasoning Theory: From Math Word Problem to Mathematical Modeling (2014-2015)
Bachelor's degree thesis @ South China Normal University
This is a thesis project required to complete a bachelor's degree in mathematics education. I review the past 20 years' literature on Quantitative Reasoning (QR) and Covariational Reasoning (CR). I discuss what it means to understand mathematical concepts quantitatively and covariationaly and how these understandings contribute to problem-solving and mathematical modeling. The literature base consists of empirical studies that investigate students' understandings of ratio, rate, proportion, slope, rate of change, and linear, quadratic, exponential, and trigonometric functions.
Undergraduate Thesis:
梁碧瑶. 关于定量思维理论的研究——从文字题到数学建模. [D]. 广州: 华南师范大学, 2015. 1-100.
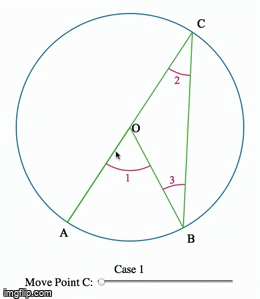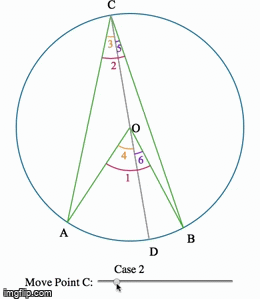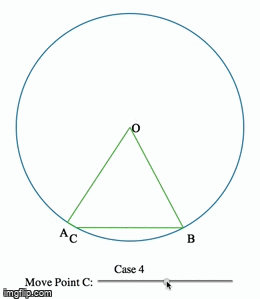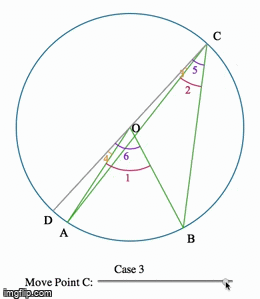
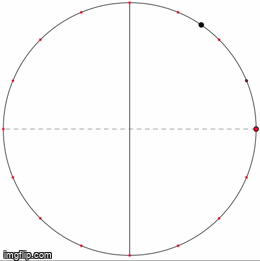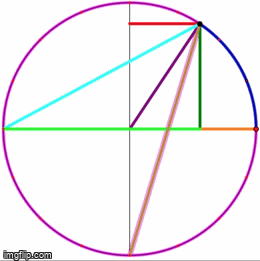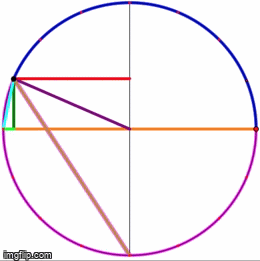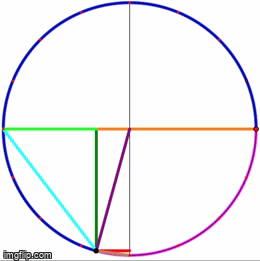
Eye-tracking Dynamic Geometric Proof (2013)
Independent study funded by Q-Center @ Kansas State University
In this project, we investigate undergraduate students' understandings of the Inscribed Angle Theorem (an angle inscribed in a circle is half of the central angle that subtends the same arc on the circle). We presented the students a pre-test, a proof-reading task, and a post-test. We used eye-tracking equipment to capture what the students paid attention to during the proof-reading task. One group of students is assigned a series of proofs accompanied by static diagrams, and another group is assigned a dynamic representation of the same proof. We asked the students to debrief on their experience right after the post-test.
Mentors: Andrew Bennett, Carlos Castillo-Garsow
Relevant Publication:
Liang, B. & Castillo-Garsow, C. (2020). Undergraduate students’ meanings for central angle and inscribed angle. The Mathematics Educator, 29(1), 53-84. https://openjournals.libs.uga.edu/tme/article/view/2093/2599