Assistant Professor @ The University of Hong Kong
PhD in Mathematics Education
Mathematics Education Researcher
Mathematics (Teacher) Educator

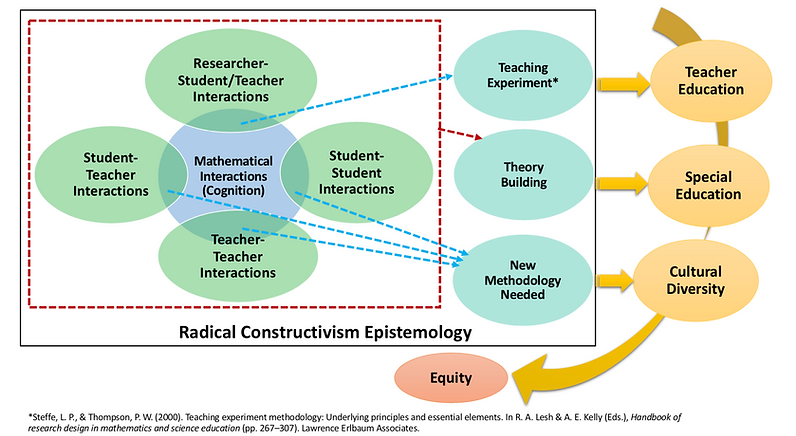
My research program is at the intersections of students' and teachers' mathematical cognition, social interactions, and teacher education. My approach to cognition centers the roles of communication and social interactions. I not only study individuals' mathematical thinking through sustained researcher-participant interactions, but I also study individuals’ mathematical learning through social interactions with others, including student-teacher interactions, teacher-teacher interactions, and student-student interactions. My research trajectory aims to understand individuals’ ongoing constructions of mathematical knowledge in these contexts and design educational opportunities, tools, and materials that can support learning through interactions. My mission as a mathematics education researcher is to acknowledge, value, and celebrate students' and teachers' diverse mathematical ways of thinking, including those distinct from my own.
See the following descriptions of five major areas constituting my research program.
ABOUT
Student-Teacher Interactions
One line of my research is concerned with teachers' construction of knowledge of students' mathematical meanings in the context of student-teacher interaction. Using a cognitive lens to approach student-teacher interaction, I focus on how teachers' personal mathematical meanings influence their construction of students' meanings and how such constructions, in turn, are generative to their personal mathematical development. I look at both in-the-moment constructions and constructions occur as a result of the teachers' retrospective analysis of student thinking.
In my dissertation project, I worked with two in-service high school teachers and three of their students. The findings provided teacher educators insights into the critical mental processes involved in these teachers' learning of students' mathematics. Future research agenda along this line will involve me working with more teachers and students regarding different topical areas and in more diverse educational contexts in order to provide a generalizable account to these learning processes.
ABOUT
Teacher-Teacher Interactions
The third line of research concerns teacher-teacher interactions in the context of professional development (PD). I am interested in unfolding the cognitive mechanism of teachers' mathematical learning as they interact with their colleagues.
ABOUT
Student/Teacher Mathematical Cognition
My prior work on students' and teachers' quantitative and covariational reasoning (QR and CR) has primarily focused on functions, trigonometry, and graphing. My fourth line of inquiry focuses on extending this work to other topical areas such as linear programming (e.g., inequalities, objective function, optimization). I am also interested in the role of QR and CR in students' construction of geometric concepts and relationships (e.g., geometric similarity, transformation, proportionality, measurement). I am interested in understanding the interplay between students' physical actions of using manipulatives, physical models, and measurement/drawing tools and their construction of geometric relationships.
Many of these topics have not received sufficient attention in the literature, and my interests are sparked by my dissertation work in such contexts. My future research will focus on designing teaching experiments to investigate individuals' meanings and development of these concepts.
ABOUT
Student-Student Interactions
My second area of interest is student-student interaction. I envision this area as an extension of my dissertation project on student-teacher interaction. I conjecture that student-student interactions are also generative to students' mathematical learning. I ask the question: How do students decenter from their personal mathematical meanings and engage in understanding the perspectives of their peers? How do this engagement and the subsequent reflection on multiple ways of thinking contribute to the students' mathematical development? How may students' decentering differ from teachers' decentering? Understandings of the learning processes involved in student-student conversations will inform teachers' support and intervention for those conversations. They will also inform teacher educators in terms of training teachers to provide such support and intervention.
I also think of autistic students who are labeled as having impaired communication and social interaction skills. I am interested in investigating their mathematical leaning with an anti-deficit perspective, the affordances of peer interactions in supporting their mathematical learning, and how teachers can provide productive support to such interactions to empower students.
ABOUT
Theory and Methodology
Putting all this empirical work together, I am interested in building learning theories that characterize cognitive mechanisms of individuals' learning of others' mathematical thinking through social interactions. This requires me to incorporate the constructivist epistemology, Piagetian learning theories, and communication theories.
Further, I am intererested in investigating the applicability of these theories in international contexts. For example, what are the limitations and affordances of these theories in explaining Chinese students' and teachers' mathematical learning? Understanding what happens at the confluence of culture, radical constructivism, and mathematical learning and teaching will allow me to expand the theories to account for broader educational phenomena.
Social interaction and cognition are often treated as disparate areas. Investigating the interplay between social interaction and individual cognition motivates new methodologies. In my current and future work, I seek to develop, implement, and refine a methodology that provides individuals with opportunities to engage with others' thinking and that allows researchers to observe, hypothesize, and document the individuals' ongoing mathematical learning.